Zeitschrift
TEC21 2008|16
Kunst und Ingenieur
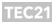
Wissenschaft und Baukunst
In der morgenländischen Baukunst haben geometrische Muster eine reiche Tradition, in der Schweizer Architekturszene schwinden seit einigen Jahren die Berührungsängste gegenüber dem Ornament. Ein «Geometrie-Ingenieur» plädiert für kunstvolle Variation statt monotone Wiederholung.
14. April 2008 - Urs B. Roth
Geometrie als Kunstform hat es im europäischen Kontext schwer. Zwar schwärmen Tausende von Touristen jährlich nach Andalusien, bewundern die Mosaike der Alhambra und die raffinierten Gewölbe der Moschee von Cordoba; doch das neu erwachte Interesse am Ornament steht in einem offensichtlichen Missverhältnis zum bescheidenen Wissen über den Aufbau dieser Werke. Geometrische Muster sind und bleiben eine fremde Welt, und so erstaunt es nicht, dass ein bescheidenes additives Dreieckmuster an der Eingangshalle eines Museums für aussereuropäische Kunst in unseren Breitengraden schon zum Medienereignis wird. Die Meister aus Granada und Isfahan hätten für diese Simplizität nur ein müdes Lächeln übrig.
Nach dem endgültigen Verschwinden des Loos’schen Ornamentsverbots scheint in der Architektur geradezu ein Durst auf Muster aufzukommen. Und so wird fleissig – und gedankenlos – appliziert: Moderne digitale Techniken machen die Sache relativ einfach. Leider aber sind Werke, in denen geometrische Ordnungen nicht nur als oberflächlicher Dekor eingesetzt werden, sondern integraler Bestandteil des Bauwerks sind, bis anhin eher rar. Zwei solche Projekte, die in Zusammenarbeit mit Herzog & de Meuron entstanden sind, sollen im Folgenden vorgestellt werden.
Mathematischer Hintergrund
Hinter jedem Ornament mit Wiederholungen steckt mathematisch gesprochen eine kongruente Abbildung: Ein Bestandteil des Ornaments wird durch Parallelverschiebung, Drehung, Spiegelung oder Gleitspiegelung mit seinem Gegenstück zur Deckung gebracht. Grünbaum und Shepard haben die mathematischen Grundlagen dieses Gebietes umfassend dargestellt.[1] Alle hier gezeigten Studien behandeln das Thema des «tiling» der Ebene, das heisst: der gesetzmässigen und lückenlosen Aufteilung der Ebene mittels weniger standardisierter Grundelemente. Diese Grundelemente sind zumeist sehr einfach geformte Polygone. Die Komplexität steckt also nicht in den Teilen selbst, sondern in deren Anordnung. In diesem Gebiet ist die Mathematik noch längst nicht zu Ende geschrieben; es gibt immer wieder Raum für neue, unerwartet komplexe Strukturen. Eine soll am Ende des Artikels vorgestellt werden. Vorweg sollen jedoch drei wichtige Kategorien von ebenen Flächenteilungen erläutert werden.
1. Die periodische Flächenteilung: Die überwiegende Zahl aller repetitiven Ornamente – darunter auch sämtliche Stoffdrucke – fallen in diese Kategorie (Bild 1). Ihr Kennzeichen ist der Rapport (RP), jener kleinste Abschnitt im Rechteck, der durch Parallelverschiebung das gesamte Muster erzeugt. Enthält der Rapport seinerseits Symmetrien, so gibt es eine noch kleinere Einheit, eine Art Stammzelle (SZ) des Musters. Sie enthält die gesamte Information des Musters; es sind aber weitere kongruente Abbildungen notwendig, um es daraus zu generieren. Das Beispiel zeigt eine erste Abwandlung eines Motivs des römischen Bodenmusters, das im 18. Jahrhundert bei Buchs ZH gefunden wurde.
2. Die aperiodische Flächenteilung generiert ein Muster, das nie durch eine Parallelverschiebung mit sich selbst zur Deckung gebracht werden kann. Die Lage jedes Teils ist bis zur Unendlichkeit festgelegt. Das Muster beruht auf dem Prinzip der Selbstähnlichkeit: Jedes Teil kann fortlaufend in kleinere Bestandteile seiner selbst unterteilt werden. Bild 2 zeigt das wohl berühmteste aperiodische Muster: «Darts & Kites» von Roger Penrose (1973). Gelb markiert sind entsprechende Teile der 1. und der 4. Generation. 2007 haben Peter J. Lu und Paul J. Steinhardt solche komplexen Geometrien an mittelalterlichen Bauwerken des Vorderen Orients nachgewiesen. [2]
3. Die quasichaotische Flächenteilung: Es handelt sich um eine eigene Schöpfung des Schreibenden (Bild 3). Auch dieses Muster ist nichtperiodisch: Es besteht aus wenigen Grundbestandteilen, deren Anordnung nicht von vornherein festgelegt ist und lokal verändert werden kann. Das quasichaotische Pattern beruht auf einer versteckten periodischen Ordnung eines lateralsymmetrischen Grundteils, das wahlweise rechts- oder linkshändig eingesetzt werden kann. Im gezeigten Beispiel ist diese Stammzelle ein mit einem rechtwinkligen Muster belegtes Drachenviereck. Dem sichtbaren Muster aus drei Quadraten und einem Rechteck liegt also eine völlig anders geartete unsichtbare Geometrie zugrunde. [3]
„Astor Place“ für Ian Schrager Hotels, New York
Herzog & de Meuron beschäftigte 2001 ein kniffliges Geometrieproblem. In Zusammenarbeit mit Rem Koolhaas / OMA entwickelten sie einen kleineren Hotelturm in Manhattan. In der Vision der Architekten war das Gebäude eine Art poröser Stein, der keine Regelmässigkeit erkennen lassen sollte. Aus Kostengründen war aber klar, dass die tragende Fassade aus standardisierten Betonelementen aufgebaut werden sollte – anscheinend ein Widerspruch. Die Frage lautete nun: Gibt es geometrische Ordnungen aus Standardelementen, die trotzdem den Eindruck von Zufall und Chaos hinterlassen? Die Suche nach diesem «wohlorganisierten Chaos» – Chaos natürlich nicht im mathematischen Sinne – führte zu einer Struktur aus sechs verschiedenen Teilen (Bild 4). Auch hier wurde das Prinzip der quasichaotischen Flächenteilung angewandt.4 Im Gegensatz zur aperiodischen Flächenteilung kann dieses Pattern lokal angepasst werden: Derselbe Umriss kann auf verschiedene Arten mit den Standardteilen gefüllt werden. Das Gebäude wurde leider nicht realisiert (Bild 5).
„Shaikh Zayed Bin Sultan Al Nahyan“-Moschee in Abu Dhabi
Bei dieser zweiten Aufgabe aus dem Büro Herzog & de Meuron war das Objekt der Studie eine riesige, von einem ortsansässigen Architekten geplante Moschee. Als der Rohbau schon sehr weit gediehen war, wurde offensichtlich, dass das Projekt schwerwiegende funktionale und gestalterische Mängel aufwies. Herzog & de Meuron erhielten daraufhin den Auftrag, Massnahmen für die Rettung des Baus vorzuschlagen. Ein Problem stellte ausgerechnet der Hauptraum dar: eine Gebetshalle für 6000 Gläubige. Er ist durch 24 massive Stützenbündel geprägt, die drei leicht verschieden grosse Kuppeln tragen. Diese Stützen stehen beliebig im Raum und kommen auch der Forderung nach regelmässigen Gebetsplätzen in die Quere. Herzog & de Meuron schlugen eine radikale Lösung vor: Könnte man die Kuppeln nicht neu abfangen? Ein regelmässiger Stützenwald – analog zur Moschee in Cordoba – gäbe dem Gebetsraum die nötige Regularität und Ruhe. In der Höhe würden sich die Stützen verzweigen und die Last der schon gebauten Kuppeln übernehmen (Bild 6). Der Bauherr lehnte jedoch ab: Die Stützen sollten da bleiben, wo sie sind. Die neue Fragestellung bezog sich auf die Geomerie: Gäbe es eine geometrische Ordnung, die im Nachhinein die seltsame Stützenstellung sinnvoll einbinden könnte? Mit Herzog & de Meuron wurde eine klare Arbeitsteilung vereinbart: Ich übernahm die Aufgabe des «Geometrie-Ingenieurs», sie übersetzten die entstandenen geometrischen Ordnungen in architektonische Elemente. Zwei unterschiedliche Lösungsansätze sollen im Folgenden vorgestellt werden:
1. Polygons: Es handelt sich um ein Puzzle aus zwei gleichschenkligen Dreiecken. Die Kombinationen dieser zwei Elemente ergeben eine riesige Vielfalt an Unterformen; die Teile sind aber auch dazu geeignet, eine gerade Raumbegrenzung zu bilden. Interessant ist das lateralsymmetrische Sechseck als Basis der Viererstützen: Es ist ein echtes Loch im Gewebe, das sich nicht mit Standardteilen füllen liesse. Insgesamt handelt es sich hier nicht um eine systematische, sondern um eine Art Ad-hoc-Lösung – das Resultat endlosen Probierens (Bild 7).
2. Lines: Der systematische Ansatz: Könnten die 24 Stützenbündel in eine reguläre, unendlich fortsetzbare Struktur eingebunden werden? In eine Art weltumspannendes Gewebe, wie es in der Idee der «Umma der Gläubigen» repräsentiert ist? Der Ansatz ist äusserst anspruchsvoll. Entstanden ist die symmetrische Überlagerung zweier kongruenter, um 45° gedrehter rechtwinkliger Gitter. Für den Mathematiker ist sofort klar, dass eine solche Überlagerung zu einer aperiodischen Struktur führen muss.[4] In diesem Gitter sind rhythmische Abfolgen zweier Abstände abzulesen: auch hier ein Rhythmus ohne Wiederholungen. Die Integration der Stützenbündel in dieses symmetrische Geflecht ist allerdings nur teilweise geglückt (Bild 8). Eine nachträgliche Analyse der Studie brachte Erstaunliches zutage: Zerlegt man dieses unendlich fortsetzbare Linienmuster in seine Elementarteile, so findet man ein Hintergrundpattern aus 4 Elementen: Quadrat, Drachenviereck, Sechseck und reguläres Achteck. Wieder kommt das Prinzip der Selbstähnlichkeit zum Zuge (Bild 9). Interessant ist die Anordnung der Sechsecke: Sie bilden geschlossene fraktale Ringe. Diese Struktur ist nicht eine Erfindung des Schreibenden, sondern ein mathematisches Gebilde, das per se existiert.[5] Leider ist auch dieses spannende Projekt schon früh abgebrochen worden. Ungewiss bleibt, was Herzog & de Meuron aus diesen geometrischen Ordnungen entwickelt hätten. Sicher ist, dass Abu Dhabi das geeignete kulturelle Umfeld für die Kunst der Geometrie gewesen wäre!
Ausblick
Alle hier vorgestellten geometrischen Ordnungen gehen vom Prinzip des Standardelements aus. Ist dieses Denken überhaupt noch zeitgemäss? Neue, digital gesteuerte Herstellungsverfahren ermöglichen die Produktion individuell geformter Teile zu durchaus vertretbaren Kosten; so ist das berühmte «Vogelnest»-Stadion von Herzog & de Meuron in Peking aus nicht standardisierten Teilen zusammengesetzt worden. Diese Debatte sollte jedoch nicht nur nach technischen und wirtschaftlichen Kriterien geführt werden. Die herrlichen Bauten des Orients könnten vielleicht die Augen öffnen für das riesige Potenzial, das in komplexen Anordnungen von ganz einfachen Grundelementen steckt. Was dort beeindruckt, ist die vollständige und selbstverständliche Verschränkung von Wissenschaft und Baukunst. In unserem kulturellen Kontext ist die Situation eine ganz andere: Mathematiker und Gestalter leben offenbar auf verschiedenen Planeten. Sollte das Interesse an komplexen geometrischen Strukturen im Bauen anhalten, wäre es jedoch wichtig, dass wieder neue Brücken geschlagen würden. Es wäre wünschenswert, dass in Zukunft der Mathematiker in der Funktion des «Geometrie-Ingenieurs» ganz selbstverständlich zum Bauteam gehören könnte.
[Urs B. Roth, dipl. Architekt ETH / SIA, Atelier für Konkrete Kunst in Zürich]
Nach dem endgültigen Verschwinden des Loos’schen Ornamentsverbots scheint in der Architektur geradezu ein Durst auf Muster aufzukommen. Und so wird fleissig – und gedankenlos – appliziert: Moderne digitale Techniken machen die Sache relativ einfach. Leider aber sind Werke, in denen geometrische Ordnungen nicht nur als oberflächlicher Dekor eingesetzt werden, sondern integraler Bestandteil des Bauwerks sind, bis anhin eher rar. Zwei solche Projekte, die in Zusammenarbeit mit Herzog & de Meuron entstanden sind, sollen im Folgenden vorgestellt werden.
Mathematischer Hintergrund
Hinter jedem Ornament mit Wiederholungen steckt mathematisch gesprochen eine kongruente Abbildung: Ein Bestandteil des Ornaments wird durch Parallelverschiebung, Drehung, Spiegelung oder Gleitspiegelung mit seinem Gegenstück zur Deckung gebracht. Grünbaum und Shepard haben die mathematischen Grundlagen dieses Gebietes umfassend dargestellt.[1] Alle hier gezeigten Studien behandeln das Thema des «tiling» der Ebene, das heisst: der gesetzmässigen und lückenlosen Aufteilung der Ebene mittels weniger standardisierter Grundelemente. Diese Grundelemente sind zumeist sehr einfach geformte Polygone. Die Komplexität steckt also nicht in den Teilen selbst, sondern in deren Anordnung. In diesem Gebiet ist die Mathematik noch längst nicht zu Ende geschrieben; es gibt immer wieder Raum für neue, unerwartet komplexe Strukturen. Eine soll am Ende des Artikels vorgestellt werden. Vorweg sollen jedoch drei wichtige Kategorien von ebenen Flächenteilungen erläutert werden.
1. Die periodische Flächenteilung: Die überwiegende Zahl aller repetitiven Ornamente – darunter auch sämtliche Stoffdrucke – fallen in diese Kategorie (Bild 1). Ihr Kennzeichen ist der Rapport (RP), jener kleinste Abschnitt im Rechteck, der durch Parallelverschiebung das gesamte Muster erzeugt. Enthält der Rapport seinerseits Symmetrien, so gibt es eine noch kleinere Einheit, eine Art Stammzelle (SZ) des Musters. Sie enthält die gesamte Information des Musters; es sind aber weitere kongruente Abbildungen notwendig, um es daraus zu generieren. Das Beispiel zeigt eine erste Abwandlung eines Motivs des römischen Bodenmusters, das im 18. Jahrhundert bei Buchs ZH gefunden wurde.
2. Die aperiodische Flächenteilung generiert ein Muster, das nie durch eine Parallelverschiebung mit sich selbst zur Deckung gebracht werden kann. Die Lage jedes Teils ist bis zur Unendlichkeit festgelegt. Das Muster beruht auf dem Prinzip der Selbstähnlichkeit: Jedes Teil kann fortlaufend in kleinere Bestandteile seiner selbst unterteilt werden. Bild 2 zeigt das wohl berühmteste aperiodische Muster: «Darts & Kites» von Roger Penrose (1973). Gelb markiert sind entsprechende Teile der 1. und der 4. Generation. 2007 haben Peter J. Lu und Paul J. Steinhardt solche komplexen Geometrien an mittelalterlichen Bauwerken des Vorderen Orients nachgewiesen. [2]
3. Die quasichaotische Flächenteilung: Es handelt sich um eine eigene Schöpfung des Schreibenden (Bild 3). Auch dieses Muster ist nichtperiodisch: Es besteht aus wenigen Grundbestandteilen, deren Anordnung nicht von vornherein festgelegt ist und lokal verändert werden kann. Das quasichaotische Pattern beruht auf einer versteckten periodischen Ordnung eines lateralsymmetrischen Grundteils, das wahlweise rechts- oder linkshändig eingesetzt werden kann. Im gezeigten Beispiel ist diese Stammzelle ein mit einem rechtwinkligen Muster belegtes Drachenviereck. Dem sichtbaren Muster aus drei Quadraten und einem Rechteck liegt also eine völlig anders geartete unsichtbare Geometrie zugrunde. [3]
„Astor Place“ für Ian Schrager Hotels, New York
Herzog & de Meuron beschäftigte 2001 ein kniffliges Geometrieproblem. In Zusammenarbeit mit Rem Koolhaas / OMA entwickelten sie einen kleineren Hotelturm in Manhattan. In der Vision der Architekten war das Gebäude eine Art poröser Stein, der keine Regelmässigkeit erkennen lassen sollte. Aus Kostengründen war aber klar, dass die tragende Fassade aus standardisierten Betonelementen aufgebaut werden sollte – anscheinend ein Widerspruch. Die Frage lautete nun: Gibt es geometrische Ordnungen aus Standardelementen, die trotzdem den Eindruck von Zufall und Chaos hinterlassen? Die Suche nach diesem «wohlorganisierten Chaos» – Chaos natürlich nicht im mathematischen Sinne – führte zu einer Struktur aus sechs verschiedenen Teilen (Bild 4). Auch hier wurde das Prinzip der quasichaotischen Flächenteilung angewandt.4 Im Gegensatz zur aperiodischen Flächenteilung kann dieses Pattern lokal angepasst werden: Derselbe Umriss kann auf verschiedene Arten mit den Standardteilen gefüllt werden. Das Gebäude wurde leider nicht realisiert (Bild 5).
„Shaikh Zayed Bin Sultan Al Nahyan“-Moschee in Abu Dhabi
Bei dieser zweiten Aufgabe aus dem Büro Herzog & de Meuron war das Objekt der Studie eine riesige, von einem ortsansässigen Architekten geplante Moschee. Als der Rohbau schon sehr weit gediehen war, wurde offensichtlich, dass das Projekt schwerwiegende funktionale und gestalterische Mängel aufwies. Herzog & de Meuron erhielten daraufhin den Auftrag, Massnahmen für die Rettung des Baus vorzuschlagen. Ein Problem stellte ausgerechnet der Hauptraum dar: eine Gebetshalle für 6000 Gläubige. Er ist durch 24 massive Stützenbündel geprägt, die drei leicht verschieden grosse Kuppeln tragen. Diese Stützen stehen beliebig im Raum und kommen auch der Forderung nach regelmässigen Gebetsplätzen in die Quere. Herzog & de Meuron schlugen eine radikale Lösung vor: Könnte man die Kuppeln nicht neu abfangen? Ein regelmässiger Stützenwald – analog zur Moschee in Cordoba – gäbe dem Gebetsraum die nötige Regularität und Ruhe. In der Höhe würden sich die Stützen verzweigen und die Last der schon gebauten Kuppeln übernehmen (Bild 6). Der Bauherr lehnte jedoch ab: Die Stützen sollten da bleiben, wo sie sind. Die neue Fragestellung bezog sich auf die Geomerie: Gäbe es eine geometrische Ordnung, die im Nachhinein die seltsame Stützenstellung sinnvoll einbinden könnte? Mit Herzog & de Meuron wurde eine klare Arbeitsteilung vereinbart: Ich übernahm die Aufgabe des «Geometrie-Ingenieurs», sie übersetzten die entstandenen geometrischen Ordnungen in architektonische Elemente. Zwei unterschiedliche Lösungsansätze sollen im Folgenden vorgestellt werden:
1. Polygons: Es handelt sich um ein Puzzle aus zwei gleichschenkligen Dreiecken. Die Kombinationen dieser zwei Elemente ergeben eine riesige Vielfalt an Unterformen; die Teile sind aber auch dazu geeignet, eine gerade Raumbegrenzung zu bilden. Interessant ist das lateralsymmetrische Sechseck als Basis der Viererstützen: Es ist ein echtes Loch im Gewebe, das sich nicht mit Standardteilen füllen liesse. Insgesamt handelt es sich hier nicht um eine systematische, sondern um eine Art Ad-hoc-Lösung – das Resultat endlosen Probierens (Bild 7).
2. Lines: Der systematische Ansatz: Könnten die 24 Stützenbündel in eine reguläre, unendlich fortsetzbare Struktur eingebunden werden? In eine Art weltumspannendes Gewebe, wie es in der Idee der «Umma der Gläubigen» repräsentiert ist? Der Ansatz ist äusserst anspruchsvoll. Entstanden ist die symmetrische Überlagerung zweier kongruenter, um 45° gedrehter rechtwinkliger Gitter. Für den Mathematiker ist sofort klar, dass eine solche Überlagerung zu einer aperiodischen Struktur führen muss.[4] In diesem Gitter sind rhythmische Abfolgen zweier Abstände abzulesen: auch hier ein Rhythmus ohne Wiederholungen. Die Integration der Stützenbündel in dieses symmetrische Geflecht ist allerdings nur teilweise geglückt (Bild 8). Eine nachträgliche Analyse der Studie brachte Erstaunliches zutage: Zerlegt man dieses unendlich fortsetzbare Linienmuster in seine Elementarteile, so findet man ein Hintergrundpattern aus 4 Elementen: Quadrat, Drachenviereck, Sechseck und reguläres Achteck. Wieder kommt das Prinzip der Selbstähnlichkeit zum Zuge (Bild 9). Interessant ist die Anordnung der Sechsecke: Sie bilden geschlossene fraktale Ringe. Diese Struktur ist nicht eine Erfindung des Schreibenden, sondern ein mathematisches Gebilde, das per se existiert.[5] Leider ist auch dieses spannende Projekt schon früh abgebrochen worden. Ungewiss bleibt, was Herzog & de Meuron aus diesen geometrischen Ordnungen entwickelt hätten. Sicher ist, dass Abu Dhabi das geeignete kulturelle Umfeld für die Kunst der Geometrie gewesen wäre!
Ausblick
Alle hier vorgestellten geometrischen Ordnungen gehen vom Prinzip des Standardelements aus. Ist dieses Denken überhaupt noch zeitgemäss? Neue, digital gesteuerte Herstellungsverfahren ermöglichen die Produktion individuell geformter Teile zu durchaus vertretbaren Kosten; so ist das berühmte «Vogelnest»-Stadion von Herzog & de Meuron in Peking aus nicht standardisierten Teilen zusammengesetzt worden. Diese Debatte sollte jedoch nicht nur nach technischen und wirtschaftlichen Kriterien geführt werden. Die herrlichen Bauten des Orients könnten vielleicht die Augen öffnen für das riesige Potenzial, das in komplexen Anordnungen von ganz einfachen Grundelementen steckt. Was dort beeindruckt, ist die vollständige und selbstverständliche Verschränkung von Wissenschaft und Baukunst. In unserem kulturellen Kontext ist die Situation eine ganz andere: Mathematiker und Gestalter leben offenbar auf verschiedenen Planeten. Sollte das Interesse an komplexen geometrischen Strukturen im Bauen anhalten, wäre es jedoch wichtig, dass wieder neue Brücken geschlagen würden. Es wäre wünschenswert, dass in Zukunft der Mathematiker in der Funktion des «Geometrie-Ingenieurs» ganz selbstverständlich zum Bauteam gehören könnte.
[Urs B. Roth, dipl. Architekt ETH / SIA, Atelier für Konkrete Kunst in Zürich]
Anmerkungen
[1] Branko Grünbaum, G. C. Shepard: Tilings and Patterns. W. H. Freeman and Company, New York 1987. Dies ist das Standardwerk zur Geometrie der regulären Flächenteilungen
[2] Peter J. Lu und Paul J. Steinhardt: Decagonal and Quasi-Crystalline Tilings in Medieval Islamic Architecture, in: Science 315, 2007. An mittelalterlichen Bauwerken aus Iran, Irak, Indien und der Türkei analysieren die Autoren Patterns mit pentagonalen und dekagonalen aperiodischen Strukturen. Das Geometrieverständnis der orientalischen Meister des 12. bis 16. Jahrhunderts ist höchst beeindruckend
[3] Die Elemente des Patterns sind Quadrate mit den Seitenlängen 1, 2 und 3 und ein Rechteck mit den Seitenlängen 2 × 3. Der dargestellte kleine Ausschnitt des Patterns umfasst 36 Drachenvierecke. Es gäbe demnach 236 (= ca 7 × 1010) verschiedene Anordnungen der Rechtecke in diesem Feld
[4] Grundmodul ist hier ein lateralsymmetrisches Fünfeck. Jedes Einzelteil kann im Pattern in acht verschiedenen Lagen erscheinen. Das ist der Grund, weshalb die versteckte (periodische) Ordnung kaum zu erkennen ist
[5] Für mathematisch Interessierte: Eine Überlagerung zweier um 45° gedrehter kongruenter Strukturen zu einer Gesamtstruktur mit repetitiven Elementen muss zwangsläufi g zu einer aperiodischen Struktur führen. Grund ist der Winkel von 22.5° des Symmetrieteils, dessen Kotangens eine irrationale Zahl ist. Dieser Wert, f = √2 + 1, ist auch der Skalierungsfaktor der Selbstähnlichkeit. Interessant ist die Anordnung der Sechsecke. Sie bilden geschlossene fraktale Ringe von 8, 16, 56, 160, 488, 1456 etc. Elementen. Analog zu «Darts & Kites» von Roger Penrose hat die Struktur ein Symmetriezentrum. Es ist der Schnittpunkt von 8 Symmetrieachsen. Die Struktur entwickelt sich alternierend in 2 Varianten: mit Achteck oder 8 Drachenvierecken im Zentrum
[1] Branko Grünbaum, G. C. Shepard: Tilings and Patterns. W. H. Freeman and Company, New York 1987. Dies ist das Standardwerk zur Geometrie der regulären Flächenteilungen
[2] Peter J. Lu und Paul J. Steinhardt: Decagonal and Quasi-Crystalline Tilings in Medieval Islamic Architecture, in: Science 315, 2007. An mittelalterlichen Bauwerken aus Iran, Irak, Indien und der Türkei analysieren die Autoren Patterns mit pentagonalen und dekagonalen aperiodischen Strukturen. Das Geometrieverständnis der orientalischen Meister des 12. bis 16. Jahrhunderts ist höchst beeindruckend
[3] Die Elemente des Patterns sind Quadrate mit den Seitenlängen 1, 2 und 3 und ein Rechteck mit den Seitenlängen 2 × 3. Der dargestellte kleine Ausschnitt des Patterns umfasst 36 Drachenvierecke. Es gäbe demnach 236 (= ca 7 × 1010) verschiedene Anordnungen der Rechtecke in diesem Feld
[4] Grundmodul ist hier ein lateralsymmetrisches Fünfeck. Jedes Einzelteil kann im Pattern in acht verschiedenen Lagen erscheinen. Das ist der Grund, weshalb die versteckte (periodische) Ordnung kaum zu erkennen ist
[5] Für mathematisch Interessierte: Eine Überlagerung zweier um 45° gedrehter kongruenter Strukturen zu einer Gesamtstruktur mit repetitiven Elementen muss zwangsläufi g zu einer aperiodischen Struktur führen. Grund ist der Winkel von 22.5° des Symmetrieteils, dessen Kotangens eine irrationale Zahl ist. Dieser Wert, f = √2 + 1, ist auch der Skalierungsfaktor der Selbstähnlichkeit. Interessant ist die Anordnung der Sechsecke. Sie bilden geschlossene fraktale Ringe von 8, 16, 56, 160, 488, 1456 etc. Elementen. Analog zu «Darts & Kites» von Roger Penrose hat die Struktur ein Symmetriezentrum. Es ist der Schnittpunkt von 8 Symmetrieachsen. Die Struktur entwickelt sich alternierend in 2 Varianten: mit Achteck oder 8 Drachenvierecken im Zentrum
Für den Beitrag verantwortlich: TEC21
Ansprechpartner:in für diese Seite: Judit Solt